Ablowitz-Ladik方程是非线性薛定谔(NLS)方程的完全可积离散化形式,是重要的非线性数学物理方程。由于非线性性质,其初值问题一般不存在解析解,从而渐近分析对研究其初值问题解的性质具有重要意义。然而,在低正则初值条件下(即初值属于一个加权离散l2空间),由于其渐近分析过程中产生的反射系数光滑性减弱,其渐近分析的研究一直存在很大困难。
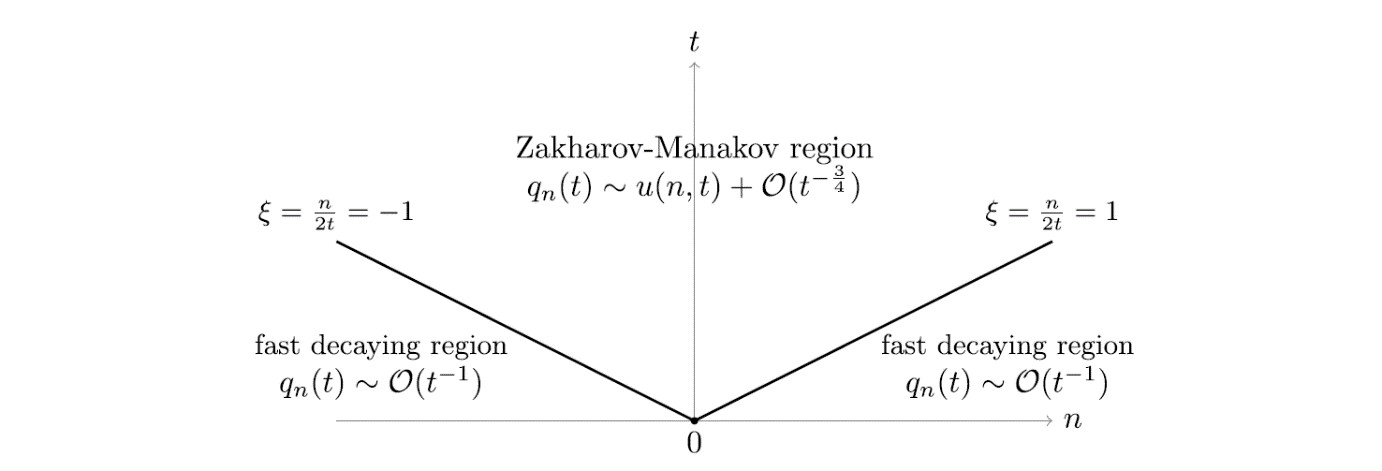
近期,jinnianhui金年会·(金字招牌)诚信至上青年教师陈美森博士与复旦大学范恩贵教授和深圳大学贺劲松教授在国际纯数学领域的顶尖期刊《Advances in Mathematics》发表了题为“Long-time asymptotics for the defocusing Ablowitz-Ladik system with initial data in lower regularity”的重要学术成果。论文引入一种dbar最速下降方法,旨在探讨初值在低正则条件下,散焦Ablowitz-Ladik方程初值问题解的渐近性。主要思路是借助分析反射系数的性质,将初值问题对应的Riemann-Hilbert问题转换为dbar-Riemann-Hilbert问题,并通过一系列的变换来处理,最终分析得到初值问题解的渐近展开式。结论中得出在中心区域(Zakharov-Manakov区域),误差项关于时间的衰减速度为t-3/4,与NLS方程情况相符,而在两边区域(快速衰减区域),其衰减速度为t-1。
jinnianhui金年会·(金字招牌)诚信至上为该研究成果的第一完成单位,jinnianhui金年会·(金字招牌)诚信至上年轻教师陈美森博士为第一及通讯作者,该项目得到了国家自然科学基金的资助。
文章链接https://www.sciencedirect.com/science/article/pii/S0001870824002846
